Task:Define voting procedure for Community Council elections
(Added proposal) |
|||
| Line 3: | Line 3: | ||
Due to the noise generated by the voting procedure from the first election, the procedure needs to be reevaluated and a better system needs to be put in place for the next election. | Due to the noise generated by the voting procedure from the first election, the procedure needs to be reevaluated and a better system needs to be put in place for the next election. | ||
| + | |||
| + | == Proposal: RRV == | ||
| + | === Variables === | ||
| + | *<math>l</math>: number of voters | ||
| + | *<math>m</math>: number of candidates | ||
| + | *<math>n</math>: number of seats | ||
| + | *<math>i</math>: index of voters (<math>1 \le i \le l</math>) | ||
| + | *<math>j</math>: index of candidates (<math>1 \le j \le m</math>) | ||
| + | *<math>k</math>: index of seats (and rounds) (<math>1 \le k \le n</math>) | ||
| + | === Parameters === | ||
| + | A range for votes is selected by two limits, <math>a_{max}</math> and <math>a_{min}</math>. | ||
| + | Reasonable choices include: | ||
| + | *<math>a_{min}=0</math>, <math>a_{max}=1</math> (unbalanced, normalized) | ||
| + | *<math>a_{min}=-1</math>, <math>a_{max}=1</math> (balanced) | ||
| + | *<math>a_{min}=0</math>, <math>a_{max}=100</math> (unbalanced percentage; potentially useful if ratings were to be quantized) | ||
| + | The effects of the voting system are generally independent of the limits selected, but a balanced range ''may'' be preferred by some voters to permit unknown candidates to be rated 0 with known, disliked candidates rated negative. Obviously this effect may be accomplished in an unbalanced range by rating unknown candidates <math>\tfrac{a_{min} + a_{max}}{2}</math>. Some calculations are simplified by using the unbalanced, normalized range, which makes it preferable from a numerical perspective. | ||
| + | |||
| + | A ballot from voter <math>i</math> consists of <math>m</math> ratings <math>a_{ij}</math> for the <math>m</math> candidates, such that <math>a_{min} \le a_{ij} \le a_{max}</math>. | ||
| + | |||
| + | === Procedure === | ||
| + | After all ballots are collected, <math>n</math> rounds are held to choose the winners <math>w_{k}</math>, with one winner chosen per round. In the first round, the weighted ratings for each voter are initialized as <math>b_{ij1}=a_{ij}</math>. The weighted scores in each round are summed: | ||
| + | |||
| + | <math>B_{jk}=\sum_{i=1}^{l}b_{ijk}</math> | ||
| + | |||
| + | The highest-scoring candidate not yet elected wins; this is not simple to express formally: | ||
| + | |||
| + | <math>w_k = \max ( B_{jk} \ni j \notin w_{1 \cdots k-1})</math> | ||
| + | |||
| + | The weighted scores for each succeeding round are calculated by de-emphasizing ballots according to the portion in which they've already won: | ||
| + | |||
| + | <math>b_{ij(k+1)}=\frac{a_{ij}}{1+\sum_{p=1}^{k}\tfrac{a_{iw_p}-a_{min}}{a_{max}-a_{min}}}</math> | ||
| + | |||
| + | In the case of an unbalanced range (<math>a_{min} = 0</math>), <math>b_{ij(k+1)}=\frac{a_{ij}}{1+\sum_{p=1}^{k}\tfrac{a_{iw_p}}{a_{max}}}</math>, and in the normalized case (<math>a_{max} = 1</math>), <math>b_{ij(k+1)}=\frac{a_{ij}}{1+\sum_{p=1}^{k}a_{iw_p}}</math>. | ||
== Discussions == | == Discussions == | ||
Revision as of 07:36, 3 December 2008
| This is an ongoing task, planned to be completed during the current maemo.org development sprint. Any help is appreciated! Please see the talk page for discussion. |
Due to the noise generated by the voting procedure from the first election, the procedure needs to be reevaluated and a better system needs to be put in place for the next election.
Contents |
Proposal: RRV
Variables
- l: number of voters
- m: number of candidates
- n: number of seats
- i: index of voters (
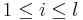 )
)
- j: index of candidates (
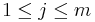 )
)
- k: index of seats (and rounds) (
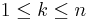 )
)
Parameters
A range for votes is selected by two limits, amax and amin. Reasonable choices include:
- amin = 0, amax = 1 (unbalanced, normalized)
- amin = − 1, amax = 1 (balanced)
- amin = 0, amax = 100 (unbalanced percentage; potentially useful if ratings were to be quantized)
The effects of the voting system are generally independent of the limits selected, but a balanced range may be preferred by some voters to permit unknown candidates to be rated 0 with known, disliked candidates rated negative. Obviously this effect may be accomplished in an unbalanced range by rating unknown candidates 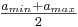 . Some calculations are simplified by using the unbalanced, normalized range, which makes it preferable from a numerical perspective.
. Some calculations are simplified by using the unbalanced, normalized range, which makes it preferable from a numerical perspective.
A ballot from voter i consists of m ratings aij for the m candidates, such that  .
.
Procedure
After all ballots are collected, n rounds are held to choose the winners wk, with one winner chosen per round. In the first round, the weighted ratings for each voter are initialized as bij1 = aij. The weighted scores in each round are summed:

The highest-scoring candidate not yet elected wins; this is not simple to express formally:

The weighted scores for each succeeding round are calculated by de-emphasizing ballots according to the portion in which they've already won:
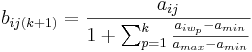
In the case of an unbalanced range (amin = 0), 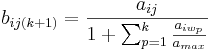 , and in the normalized case (amax = 1),
, and in the normalized case (amax = 1),  .
.
